知:韩信点兵的故事
你听说过韩信的故事吗?韩信是我国西汉朝代的开国功臣,一生立下了赫赫战功,被后人尊称为“兵家四圣”之一、“兵仙”——他不仅带兵水平一流,数学也是特别的好——传说有一次韩信带着1500名将士与楚王大将李锋交战,楚军败退,韩信带的士兵也损失了四五百人,于是韩信整顿兵马回营,不料路上又有骑兵追了过来,烟尘滚滚,声势很大,汉军军心不稳。这种情况下,身为主帅的韩信并不心慌,他先到高处查看了来犯敌人,估计数量不到五百骑,于是马上开始点兵迎敌。他命令士兵3人一排,结果多出2名;接着命令士兵5人一排,结果多出3名;他又命令士兵7人一排,结果又多出2名。韩信马上宣布:我军有1073名勇士,两倍于来犯之敌,大家奋力一搏,敌军必败!汉军见自己的统帅如此神机妙算,士气大振,一鼓作气击溃了楚军!
想一想,当时一没有纸笔,二没有电子计算器,怎么计算出来自己的士兵数量呢?看来韩信这位大将军的数学水平可是非同一般的。现在你有了 Scratch 这个强大的工具,你能用编程的方式来计算汉军士兵数量吗?
思:程序设计
实际上,“韩信点兵问题”在数学史上,是个很有名的问题,与中国古代的数学著作《孙子算经》中的“物不知数”问题相似——“今有物,不知其数,三三数之,剩二,五五数之,剩三,七七数之,剩二,问物几何?” (《孙子算经》卷下第二十六题),这类问题的解法称为“中国剩余定理”,同样的规律在西方直到18世纪才被瑞士数学家欧拉发现。我们暂且不去管《孙子算经》中怎么解决这类问题,而是考虑如何用编程来解决它。
我们可以分析题意得知,韩信的士兵在大战之前是1500名,那么打完第一仗士兵数量是不大于1500的一个数字,而这个数字要同时满足三个条件——除以3余2、除以5余3、除以7余2,那么我们只需要用循环的方式去试每一个小于1500的数字是不是满足这个条件不就可以了呢?由于满足这个条件的数字可能有多个,所以我们可以把它保存到列表中,看看哪一个数字更符合题意就能得到最合理的答案。
程序角色设计如下:
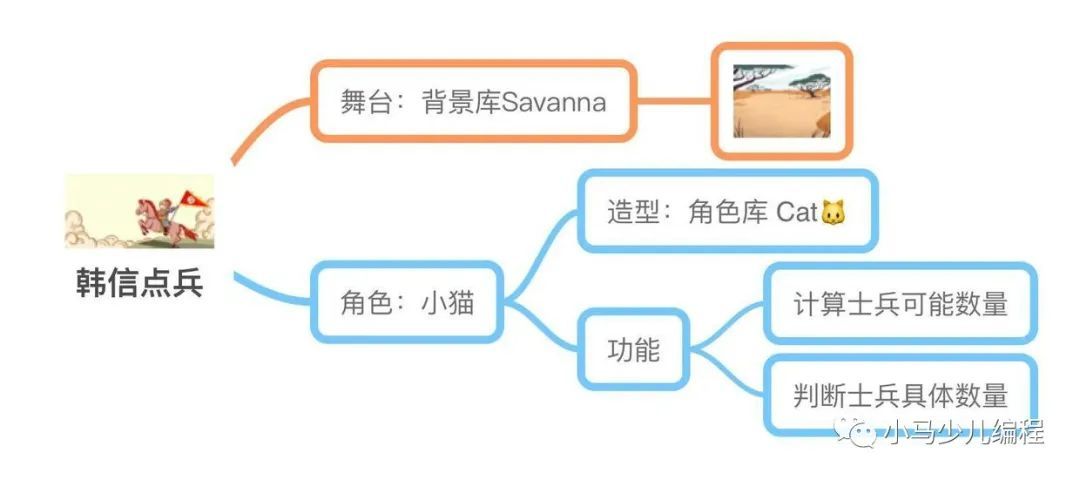
行:编程实现
1、新建 Scratch 项目,这个题目侧重于计算,所以我们不必关心背景和角色设置,直接使用默认的小猫角色就可以。我们先新建一个“可能的答案”列表,用于输出符合条件的数字,再新建一个变量“士兵数量”,并编写以下代码:

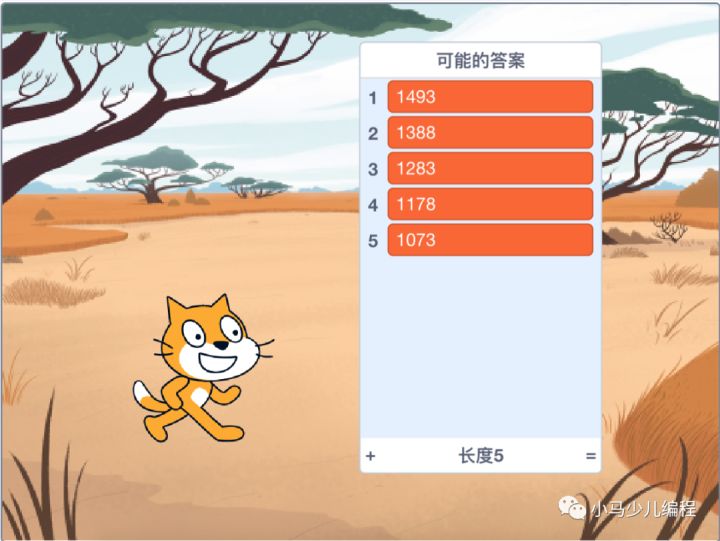
2、我们这个程序的逻辑还是很简单的,这里主要使用了取余数运算的结果进行比对。现在运行程序,你会得到 一个长长的结果列表——一共有15个符合条件的答案!

最小的23,最大的1493。那么哪个才是符合条件的答案?再回去读题,发现“韩信带的士兵也损失了四五百人”,也就是打了一仗后,韩信的士兵是1000人多一点,也就是大于1000而且最接近1000的数字,显然是1073——韩信的计算是对的!不愧是兵仙!既然有了这个限制条件,我们能否优化一下程序呢?
答案是肯定的,首先,我们可以不用再把士兵数量从1500挨个算到0了,算到1000就行,这样节约了1000次运算!其次,对于题目中连续嵌套的三个计算余数的条件,我们可以用“与”运算把它们结合起来,“与”运算也就是同时满足两个条件的意思,由于题目中有三个条件,我们可以先把第一个与第二个做“与”运算,再把结果与第三个条件做“与”运算:
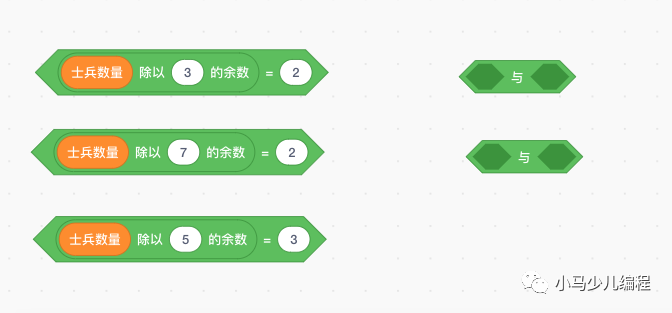
这是组合之后的条件,这样写会减少程序行数,当然你如果觉得原来的写法更容易理解,也可以保留:

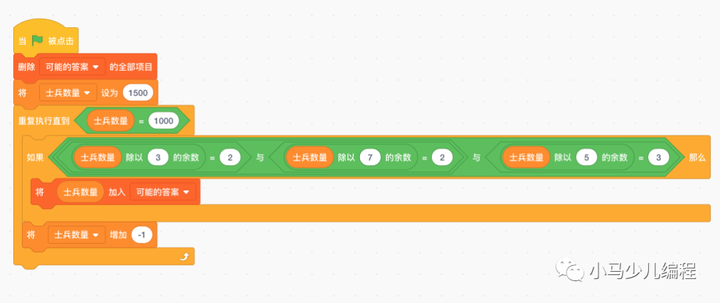
3、修改之后的程序是这样的,运行得到5个符合条件的数字,正确答案就一目了然了。
悟:总结与拓展
通过本题的解答,你会再次体会到算法的重要性——只要算法正确,程序写不了几行就能得到正确答案。那么本题使用了什么算法呢?
答案是枚举——我们在进行归纳推理时,如果逐个考察了某类事件的所有可能情况,因而得出一般结论,那么这结论是可靠的,这种归纳方法叫做枚举法。使用枚举法对计算机程序来说是相当简单的,因为计算机擅长重复性工作,但为了更快地得到正确答案,我们要尽可能地设置更合适的过滤条件,减少不必要的重复计算,比如我们在本题中只修改了一个最小士兵数量,就减少了三分之二的计算量。如果总体计算量很大,这个优化效果是非常可观的!
好了,现在试着用“枚举法”来解决下面的问题吧——
一筐苹果,如果按5个一堆放,最后多出3个;如果按6个一堆放,最后多出4个;如果按7个一堆放,还多出1个。问这筐苹果至少有多少个?
